Moved from @[email protected]
- 46 Posts
- 119 Comments

 16·11 months ago
16·11 months agoFor those curious about 1-bit computers, see Usagi Electric’s playlist:
Source Gudim:
- Twitter @like_gudim
- Nitter link
- Nitter RSS Feed: https://nitter.cz/like_gudim/rss

 2·11 months ago
2·11 months agoThanks!

 1·11 months ago
1·11 months agoI tried Pixelfed (very briefly) not so long ago. I didn’t find a propper way to search for content. How do you discover new content?
My bad, I forgot the
.rsspart.Fixed, thanks for noticing!
Almost all reddit URLs have RSS Feeds. You just need to add
.rssat the end… but before the?symbol if there is one.
I’m not a mod, so I can only suggest :).
IMHO linking to an original source is good etiquette, but that’s just my opinion.
One way to be thankful is to post links to the original source :)
Source: Alone – War and Peas – Webcomic
RSS Feed: https://warandpeas.com/feed/
Credit: u/JG_Online and u/UltraWorlds. This is the comment on the original post from reddit:
Languages are categorized by linguistic families by colours.
So Spanish and Portugese (both being Romance) are redish shades, similarly other linguistic groups share similar shades indicating these are closely related languages. (this scheme breaks down quite a bit with so many languages but generally it checks out here, if you have some linguistic background)
The map does not include labels as to no obscure the detail we put into it, so I guess this map is mainly for ppl who already have some linguistic landscape knowledge.
Area’s which have between 30 to 70% majority are shown as striped.
Area’s with a population density below 1p/km2 are shown as sparsely populated. This does not mean no one lives there but rather that a single immigrant family can add Korean to the Sahara desert, which is not what this map is about.
Languages with less than 20,000 speakers in a populated area are not shown. (This mainly to exclude the native american languages that are overwhelmingly outpopulated in states such as NY or CA)
Linguistic Isolates are shown in various grey shades.
The friend who helped me with this map is u/UltraWorlds
Source: 🚩🚩🚩 : comics
RSS Feed for u/Whoops_comics’s submissions to r/comics:
https://www.reddit.com/r/comics/search/.rss?q=author:“Whoops_comics”&include_over_18=on&restrict_sr=on&t=all&sort=newEDIT: RSS link fixed
Yep, that’s why I added the twitter source too.
Source: https://www.commitstrip.com/2015/04/27/the-eye-opener-commit/
Also on twitter:
- Twitter @CommitStrip
- Nitter link
- Nitter RSS Feed: https://nitter.cz/CommitStrip/rss
FYI: Image urls which don’t end with the file extension do not show in some frontends (like mlmym).
Removing the last part (?w=1000&ssl=1) should make it work:


 2·1 year ago
2·1 year agoHow long would you say it took you before getting a fundamental understanding?
I would say years, as with any complex activity.
I’m still forgetting things I learned 3 or even 4 times like how to do a for each loop.
You can forget in 2 different ways:
- Forget how to use something, so you need to look how to do it.
- Forget that something exists, so you cannot even look for it because you are not aware it’s a possibility.
You will forget-1 everything which you don’t use on a daily basis. That’s what internet is for. Forgetting in the 2-nd sense is much more rare and you should do something if that’s the case.
all of it feels too advanced and I get lost on how to begin
This is a bias most of us have, you overlook how easy is for you to do things that previously were impossible and focus on how hard are the things you still don’t know how to do. And computing is so complex right now that there always be “infinite” things you don’t know.
Try showing what you know to someone who doesn’t know how to code and you will get an idea of how much you have learnt :).
Anyway, I don’t really have good advice :/, just wanted to confirm that what you feel is expected. Good luck!

 4·1 year ago
4·1 year agoI think you’re confusing “arbitrarily large” with “infinitely large”. See Wikipedia Arbitrarily large vs. (…) infinitely large
Furthermore, “arbitrarily large” also does not mean “infinitely large”. For example, although prime numbers can be arbitrarily large, an infinitely large prime number does not exist—since all prime numbers (as well as all other integers) are finite.

 2·1 year ago
2·1 year agoFor integers I disagree (but I’m not a mathematician). The set of integers with infinite digits is the empty set, so AFAIK, it has probability 0.

 4·1 year ago
4·1 year agoDoesn’t it depends on whether we are talking about real or integer numbers?
EDIT: I think it also works with p-adic numbers.













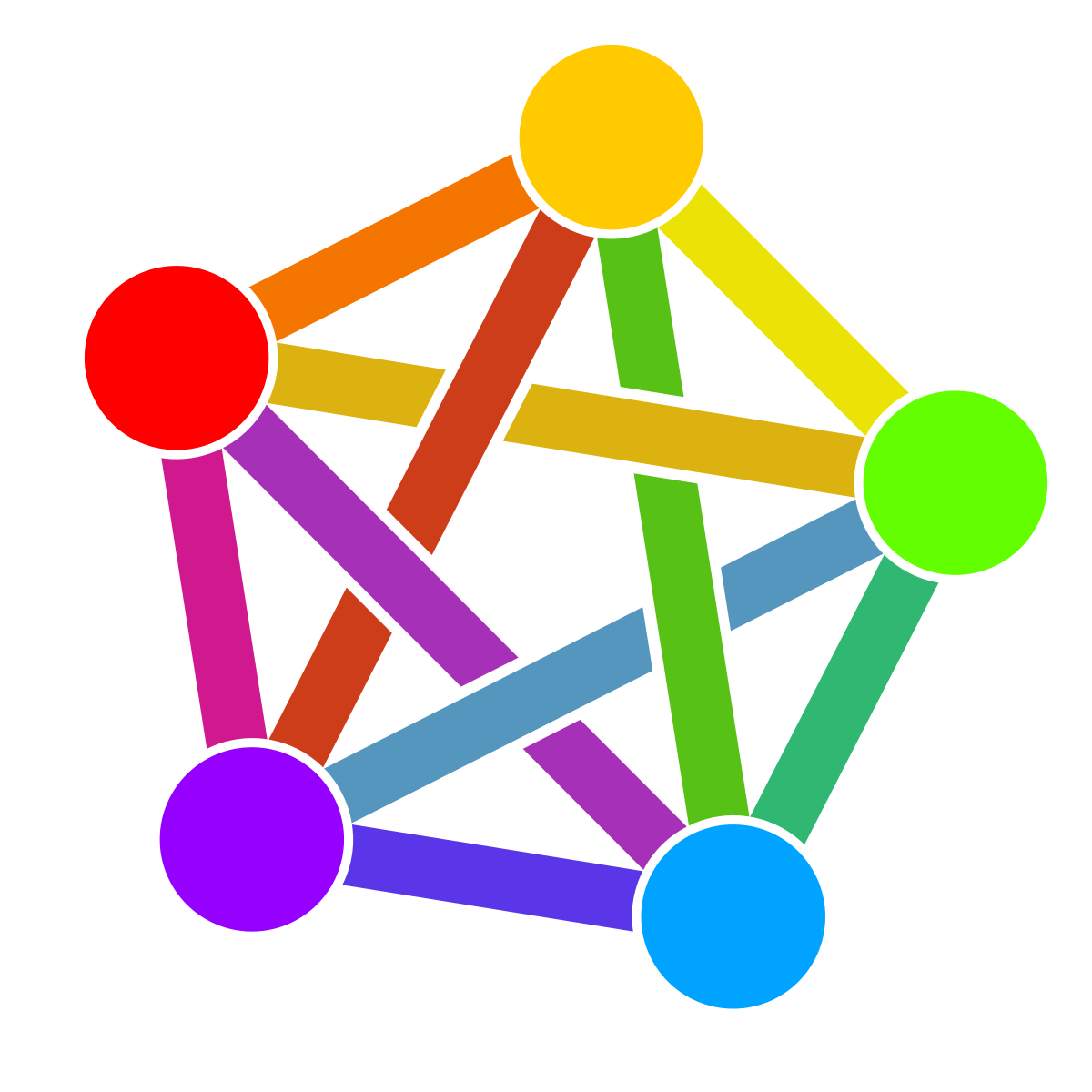
AFAIK, they are used as relays.
From https://en.wikipedia.org/wiki/1-bit_computing#1-bit
See also the playlist linked in the other comment with more explanations:
1-Bit Breadboard Computer - Usagi Electric (YouTube)