xkcd #3125: Snake-in-the-Box Problem
Title text:
Chemistry grad students have been spotted trying to lure campus squirrels into laundry hampers in the hope that it sparks inspiration.
Transcript:
Transcript will show once it’s been added to explainxkcd.com
Source: https://xkcd.com/3125/
What about goats in circular pens? A goat is tied to the fence of a circular pen. How long does the rope need to be so that the goat can reach exactly half of the pen’s area? What sounds like a high school math problem was eventually solved in 2020 via complex analysis.
Here’s the answer:

I feel like the answer should be much simpler than that equation salad.
Equation salad? It’s elegant. Well, according to my father who was a math professor.
Deriving that monstrosity must be something out of a grad school horror novel.
The difficulty is that the goat is tied to the fence.
It would be a lot easier to put a pole in the center of the circle.
The length of the rope would then be 0.5 x sqr(2) x fence radius.
What’s really neat about this problem is that the 3D example, a bird in a cage, was solved sooner and is much simpler
I thought “wtf” after reading the problem, said “wtf” out loud after reading this comment. pretty neat :)
Randall forgot psychology, which has involved a ton of putting animals in boxes…
In computer science, you steal the box from the psych department and put children in it so you can sell them loot crates
Also zoology
I guess a key thought experiment doesn’t qualify as a reason, and also we are supposed to conveniently forget about putting spherical cows in a vacuum just because.
We have one for combinatorics: Ask Fibonacci about his rabbits.

Either I’m misunderstanding the problem or a length of 8 is possible.
Edit: found my mistake, far left edge has two non-consecutive segments on adjacent corners. Leaving this up in case anyone else tries for a better score.

This should do it, or am I missing something?
The head would share an edge with the arse (supposing the arse is on the first bend from the tail).
I’m just nodding along and hoping no one notices i don’t know what’s happening
you mean the snake didn’t know internal affairs was on to them the entire time?
Unless your snake is an ouroboros, I don’t think folks will count the head and tail as consecutive
The head and tail aren’t adjacent if you only look at my blue line and not the original. But my attempt fails due to the far left edge.
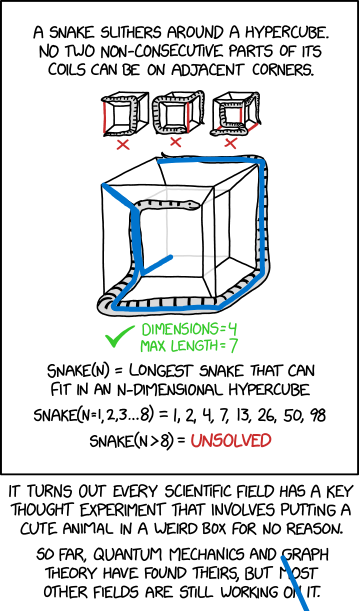
10?
Your snake has two heads.
Also, one of them shares an edge with the tail.
There really is an xkcd for everything.
I’d expect something around ~200 for n=9 and ~400 for n=10, but I imagine this is too big to be brute forced by raw computing
Some lower bounds have been established: https://oeis.org/A099155
Wow, it already lists the xkcd in the links section. I have a feeling that snake is gonna bite its tail soon.
Some trivial bounds: F(n-1) + 1 <= F(n) <= F(n-1) * 2 + 1.
Also F(n) <= 2^(n-1)
I’d think that it’s not “too much to be brute forced”, but probably no one has thrown enough resources at that recently
With each additional dimension, the amount of possible combinations grows exponentially. Without serious optimization efforts, computation requirements get prohibitive very, very fast
I’m still trying to fill that hotel with infinite monkeys
In biology it’s less of a “thought” experiment
More of a “This is how we weigh a critter that won’t stay put for more than .3 seconds”
My combinatorics professor used gnomes!
[This comment has been deleted by an automated system]
Took me a while to follow that too! The three examples of fails at the top each show instances where there are non-consecutive parts of the snake on adjacent corners - it’s the lines highlighted in red.
Basically no two parts of the snake that aren’t directly joined to each other in the snake are allowed to be on corners which are only a line apart.
I think.
Any two coils that are not directly connected. For example, suppose we number from the head, coil 1, 2, 3, 4. Then pairs that are not directly connected are: (1, 3), (1, 4), (2, 4). The endpoints of these pairs of segments cannot be connected by an edge of the cube.










